Cursus toegepaste statistiek en data-analyse
Inleiding Cursus toegepaste statistiek en data-analyse
Tridata, instituut voor toegepaste statistiek en data-analyse, biedt een vijfdaagse cursus statistiek aan, waarin een uitgebreid palet aan statistische kennis en vaardigheden aan bod komen. De toepasbaarheid van deze kennis en vaardigheden staat hierbij centraal. Voor zowel cursisten met basiskennis als voor meer ervaren cursisten biedt de cursus toegepaste statistiek en data-analyse dan ook de unieke mogelijkheid om binnen een zeer korte periode fundamentele en zeer waardevolle onderzoeksvaardigheden eigen te maken.
Bekijk ook de cursus statistiek met R
Inhoud Cursus toegepaste statistiek en data-analyse
In deze cursus statistiek wordt ingegaan op het onderzoeksproces dat een cursist doorloopt. De cursist krijgt bruikbare handvatten aangereikt, waardoor hij/zij na deze cursus gefundeerde uitspraken kan doen. Er wordt stilgestaan bij het verschil tussen beschrijvende en verklarende statistiek en er wordt aandacht besteed aan het correct formuleren en het operationaliseren van een onderzoeksvraag. De cursist krijgt inzicht in de wijze waarop de vertaling van de onderzoeksvraag naar analyses kan worden gemaakt. In rap tempo wordt kennisgemaakt met het computerprogramma SPSS, waarbij in de daaropvolgende dagen veelvuldig zal worden geoefend met data. In de cursus wordt gebruik gemaakt van Excel en SPSS.
Eindtermen
Na afronding van de cursus statistiek:
– heeft de cursist kennis en inzicht in het verloop van het onderzoeksproces;
– heeft de cursist inzicht in statistische methoden en basis en geavanceerde technieken;
– is de cursist in staat de keuze voor een specifieke analyse adequaat te kunnen verantwoorden;
– heeft de cursist grondige kennis van de achtergrond van de behandelde statistische analyses;
– is de cursist in staat analyses verantwoord toe te passen op concrete onderzoeksvragen, alsmede
de hieruit voortkomende resultaten zelfstandig te kunnen interpreteren
– heeft de cursist concrete methoden in handen voor het eigen onderzoek
Programma cursus toegepaste statistiek en data-analyse
In de cursus statistiek wordt gewerkt met korte informatieblokken, afgewisseld met praktijkopdrachten.
Dag 1:
Wat is statistiek, wanneer en hoe kan het worden gebruikt (basisbegrippen statistiek)
Statistiek in bredere context
Waarom wordt statistiek gebruikt
Steekproef
Standaard deviatie
Soorten steekproeven
Oefenen sd
Beschrijvende statistiek en data-inspectie
Het proces
Inferentiële en descriptieve statistiek
Descriptieve maten, centrummaten, spreidingsmaten
Scoreverdelingen, kansverdeling en betrouwbaarheidsinterval
Scheefheid en gepiektheid
Meetniveaus
Data-inspectie (missende waarden en extreme waarden)
Boxplots
Scatterplots
Dag 2:
Wanneer wordt gekozen voor welke analysemethode (statistische toets, algemeen)
Begrijpend leren lezen; keuzebepaling statistische analyse
Hypotheses testen
Betrouwbaarheidsintervallen
Significantie
Criteria voor meetkwaliteit (validiteit en betrouwbaarheid)
Verschil parametrische en non-parametrische tests
Dag 3:
Analyse toegelicht, meer in de diepte (t-test, ANOVA)
Onderzoeksvraag bij t-test
Verschillende soorten t-test toegelicht
One-sample t-test
Dependent sample t-test
Independent sample t-test
Analyseren in excel en/of SPSS
Interpretatie t-test
Onderzoeksvraag bij univariate variantieanalyse (ANOVA)
Univariate variantieanalyse (ANOVA) toegelicht
Post-hoc analyse
Analyse ANOVA in excel en/of SPSS
Intepretatie ANOVA
Dag 4:
Analyse toegelicht (tweewegs variantieanalyse, MANOVA)
Onderzoeksvraag bij tweewegs variantieanalyse
Tweewegs variantieanalyse toegelicht
Analyseren in excel en/of SPSS
Interpretatie tweewegs variantieanalyse
Onderzoeksvraag bij MANOVA
MANOVA toegelicht
Analyseren in excel en/of SPSS
Interpretatie MANOVA
Dag 5:
Analyse toegelicht (correlatie en regressie-analyse)
Het verband tussen variabelen
Het bereik van correlatie
Verschillende soorten correlaties
Causaliteit en correlatie
Analyses waarmee voorspellingen gedaan kunnen worden
Regressieanalyse
Het regressiemodel
R square
F-toets
Verschillende methodes (blockwise, stepwise, forces entry)
Interpretatie regressie
Analyses uitvoeren op de eigen dataset en de uitkosten interpreteren en rapporteren
Doelgroep
De cursus toegepaste statistiek en data-analyse wordt afgestemd op informatieanalisten, data-analisten, businessanalisten, adviseurs en iedereen die zich bezighoudt met het vastleggen en het analyseren van informatiebehoeften binnen een organisatie.
Docent
Dr. S. (Selene) Fagel studeerde Neuropsychologie aan de Universiteit Utrecht en was werkzaam als onderzoeksmedewerker bij Altrecht en het VU Medisch Centrum.
Mevrouw dr. Fagel was tevens verbonden aan de Vrije Universiteit (VU) als postdoc. In 2013 promoveerde zij aan de universiteit van Leiden op een proefschrift getiteld ‘Childhood psychopathology & development of adult schizotypal symptoms’. Zij heeft ruime ervaring in het geven van onderwijs en het verzorgen van trainingen in o.a. statistiek en data-analyse. Zij is v.a. 2008 verbonden aan Tridata als adviseur en trainer en als onderzoeker aan de Inspectie van Onderwijs. Mevrouw dr. Fagel is een van onze acht ervaren statistiek docenten.
Cursuslocatie
Europalaan 400 | 3526KS Utrecht
In-company training
De statistiek cursus kan ook in-company worden gegeven. Een in-company training, ook wel in-house training of bedrijfstraining, is een training die binnen jouw organisatie plaatsvindt. Hebben meerdere collega’s in uw organisatie dezelfde leervraag? Dan is een in-company training zeer geschikt. Onze trainingsprogramma’s stemmen we af op leerwensen en –doelen van jou en je collega’s. Neemt u voor een maatwerkofferte contact op met Tridata.
Cursusdata
28 maart, 4 april, 11 april, 18 april, 25 april 2024.
16 mei, 23 mei, 30 mei, 6 juni, 13 juni 2024
Lestijden
De lestijden zijn van 9:15 tot 16:00, met uitloop tot uiterlijk 16:15.
Studiebelasting
De cursus toegepaste statistiek en data analyse duurt 5 dagen. Per week kun je rekenen op 8 uur studielast, op de cursusdag zelf. Daarnaast ben je in je vrije tijd per week nog 2-4 uur bezig met de voorbereiding en verwerking van de cursusdag. Dit is afhankelijk van de intensiviteit van de lesstof en jouw eigen opleidingsachtergrond.
Kosten en inschrijving
De kosten van de 5 daagse cursustoegepaste statistiek en data-analyse bedragen € 2650. De cursusprijs is vrijgesteld van BTW (BTW-tarief 0%) en is inclusief cursusmateriaal, deelnamecertificaat, koffie/thee, inclusief lunches en inclusief boek.
Vervolgcursus
Uitgewerkte voorbeeld (met Excel) van een van de onderwerpen die tijdens de cursus aan bod zullen komen
Variantieanalyse uitvoeren in Excel
Variantieanalyse,een begrip uit de statistiek, vaak aangeduid als ANOVA, is een toetsingsprocedure om na te gaan of de populatiegemiddelden van twee of meer groepen van elkaar verschillen.
A. Overzicht van ANOVA
B. Stap-voor-stap instructies voor het uitvoeren van ANOVA in Excel
C.Excel output interpreteren
A. Overzicht van ANOVA
We willen vaak weten of de gemiddelden van twee normaal verdeelde populaties aan elkaar gelijk zijn. Bijvoorbeeld, verdienen vrouwen even veel als mannen? Dit is makkelijk te achterhalen door een onafhankelijke t-test voor twee steekproeven uit te voeren. Wanneer we nu willen weten of Friezen, Groningers en Limburgers gemiddelde hetzelfde verdienen dan kunnen we een variantieanalyse gebruiken, ook wel aangeduid als ANOVA (Engels: ‘ANalysis Of VAriance’). Dit is een toetsingsprocedure om na te gaan of de populatiegemiddelden van twee of meer groepen van elkaar verschillen. Dit in tegenstelling tot een t-test waarbij we analyseren of twee steekproefgemiddeldes van elkaar verschillen.
Een eenvoudig voorbeeld zal de gedachtegang verduidelijken.
We vragen ons af of er tussen drie verschillende beroepsgroepen systematische verschillen zijn wat betreft werkgerelateerde stress. We vergelijken : OG makelaars, advocaten en effectenmakelaars.
De onderzoeksvraag die je kunt beantwoorden met behulp van de ANOVA is de volgende:
Is de werkgerelateerde stress gemiddeld genomen dezelfde voor de drie groepen, of zijn er systematische verschillen?
Hieruit volgt direct de vraag of er ook tussen de drie groepen verschillen zijn. Of bijvoorbeeld de stress bij de makelaars anders is dan de stress bij de advocaten.
Natuurlijk zullen de gemiddelden van de drie groepen niet precies aan elkaar gelijk zijn. We vragen ons daarom af of deze verschillen tussen de groepen vergelijkbaar zijn met, of veel groter zijn dan de verschillen binnen de groepen. Om dit te analyseren wordt middels steekproeven van de drie groepen de totale “variantie”, die een maat is voor de spreiding van de geobseerveerde waarden, in twee componenten geanalyseerd , namelijk de variantie binnen de drie groepen en de variantie tussen de drie groepen.
Het onderzoek ziet erals volgt uit:
De drie groepen (makelaars, advocaten en effectenmakelaars) kregen elk 15 vragen voorgelegd over de mate van stress die zij ondervonden tijdens hun werk. Deze 15 vragen werden op een vijf punts-schaal geevalueerd, waarbij een hoger getal een hogere mate van stress indiceert. De reacties zijn per beroepsgroep samengevoegd om tot een numerieke maat voor werkgerelateerde stress te komen.
De gevonden resultaten zijn hieronder in het Excel-bestand weergegegeven.
B. Stap-voor-stap instructies voor het uitvoeren van ANOVA in Excel
| OG makelaars | advocaten | effectenmakelaars |
| 81 | 43 | 65 |
| 48 | 63 | 48 |
| 68 | 60 | 57 |
| 69 | 52 | 91 |
| 54 | 54 | 70 |
| 62 | 77 | 67 |
| 76 | 68 | 83 |
| 56 | 57 | 75 |
| 61 | 61 | 53 |
| 65 | 80 | 71 |
| 64 | 50 | 54 |
| 69 | 37 | 72 |
| 83 | 73 | 65 |
| 85 | 84 | 58 |
| 75 | 58 | 58 |
Het bovenstaande is een voorbeeld van one-way ANOVA, ook wel éénweg-variantieanalyse. Er is sprake van één factor (stress), en drie niveaus (de drie groepen,: nl OG makelaars, advocaten en effectenmakelaars).
Stap 1: Formuleer de hypothesen
H0: μ1 = μ2 = μ3
H1 : μ1 # μ2 # μ3
Waarbij
H0 = nulhypothese
H1 = alternatieve hypothese
μ1 = het gemiddelde van groep 1,
μ2 = het gemiddelde van groep 2,
μ3 = het gemiddelde van groep 3
De nulhypothese die men bij deze vraagstelling toetst is de volgende: Het gemiddelde van de populaties waaruit de steekproeven respectievelijk komen is gelijk.
De alternatieve hypothese is: Er is een significant (statistisch merkbaar) verschil tussen de gemiddelden van de drie groepen.
Als de nulhypothese waar is, dan zal de “variantie tussen de groepen (bijna) gelijk zijn aan de” variantie binnen de groepen. ”
De testgrootheid van de ANOVA is de F, waarbij F is gedefinieerd als de verhouding van de twee varianties (tussen en binnen de groepen).
Stap 2: Kies een kritische waarde (α) van bijvoorbeeld 0.05 of 0.10 voor de test.
Stap 3: Bereken de F-statistiek met behulp van Excel data-analyse.
Klik op Extra en kies DATA ANALYSE, volgens kiest u het juiste type van ANOVA:
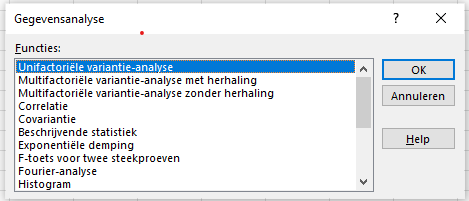
Er zijn 3 soorten ANOVA in Excel. “Single factor” ANOVA is hetzelfde als “one-way” ANOVA. Dat is wat we hebben in dit voorbeeld, omdat we alleen één factor (stress) in ogenschouw nemen. Excel kan omgaan met een willekeurig aantal groepen, zolang ze maar in kolommen zijn weergegeven. Na het kiezen van “ANOVA: Single Factor” zie je het volgende:
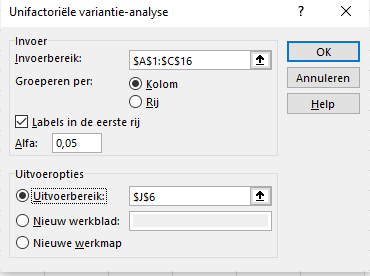
In “Input Range” selecteert u het bereik A1:C16, incl. de labels op de eerste Rij.
Labels in first Row aanvinken.
Geef de kritische waarde (α) aan (standaard staat het op 0.05).
Kies voor New Worksheet en klik vervolgend op OK waarna de volgende output verschijnt.
| Unifactoriële variantie-analyse | ||||
| SAMENVATTING | ||||
| Groepen | Aantal | Som | Gemiddelde | Variantie |
| OG makelaars | 15 | 1016 | 67,73 | 117,64 |
| advocaten | 15 | 917 | 61,13 | 179,98 |
| effectenmakelaars | 15 | 987 | 65,80 | 137,17 |
| Variantie-analyse | ||||||
| Bron van variatie | SS | df | MS | F | P-value | F crit |
| Tussen groepen | 345,38 | 2 | 172,69 | 1,19 | 0,31 | 3,22 |
| Binnen groepen | 6087,07 | 42 | 144,93 | |||
| Totaal | 6432,44 | 44 |
| SS | Kwadratensom |
| df | Vrijheidsgraden |
| MS | Gemiddelde kwadraten |
| F | F |
| P-value | P-waarde |
| F crit | Kritische gebied van F-toets |
C. Excel output interpreteren
Het gemiddelde niveau van stress wordt geïnterpreteerd voor elke groep, waarbij wordt opgemerkt dat het gemiddelde stressniveau hoger is bij makelaars dan bij effectenmakelaars en advocaten.
De F-waarde wordt vergeleken met de kritische waarde (F crit) bij het gegeven significantieniveau (α = 0.05).
In dit geval is de F-waarde (1,19) kleiner dan de kritische waarde (3,22) bij α = 0.05, wat resulteert in een p-waarde van 0,31 (P-value = 0,31).
Omdat de p-waarde (0,31) hoger is dan het gekozen significantieniveau (0,05), wordt de nulhypothese (H0: μ1 = μ2 = μ3) niet verworpen. Dit betekent dat er geen significant verschil is tussen de gemiddelde stressniveaus van de drie beroepsgroepen, en de waargenomen verschillen kunnen verklaard worden door toeval.
Samengevat
De resultaten tonen aan dat er geen significant verschil is tussen de gemiddelde stressniveaus van de drie beroepsgroepen, en de waargenomen verschillen zijn hoogstwaarschijnlijk het gevolg van toeval.
